In the previous post we visualised the quarterly returns for the 30 components of the DJIA between 2005-2009. After ranking quarterly performance of each stock , we proceeded to regress excess monthly log returns on the Fama & French factors in both the standard OLS and the more robust QRS frameworks. This post will focus on applying an input- oriented -variable- returns- to- scale DEA model to requisite inputs and outputs for each stock. While the regression coefficients extracted from the OLS and QRS procedures for each year constitute the inputs to the DEA model, the annualised returns for each stock represent associated outputs for each DMU. Before these attributes can be passed to the DEA model, it is first necessary to standardise and rescale them. The methodology is detailed in the links provided in the previous post.
l
windows()
par(mai=c(0.1,0.5,0.5,0.5),mfrow=c(6,1))
barplot(main="DEA applied to Quantile inputs",cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.05[,1],col=ifelse(round(t(eff.05[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[1],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.06[,1],col=ifelse(round(t(eff.06[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[2],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.07[,1],col=ifelse(round(t(eff.07[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[3],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.08[,1],col=ifelse(round(t(eff.08[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[4],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.09[,1],col=ifelse(round(t(eff.09[,1])[1,],2)<1.00,"red","blue"),las=2)
mtext(side=4,Years[5],cex=0.7)
plot.new()
legend("center",title="Data Envelopement Analysis",fill=c("blue","red"),legend=c("Efficient","Inefficient"),ncol=2)
windows()
par(mai=c(0.1,0.5,0.5,0.5),mfrow=c(6,1))
barplot(main="DEA applied to OLS inputs",cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.ols.05[,1],col=ifelse(round(t(eff.ols.05[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[1],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.ols.06[,1],col=ifelse(round(t(eff.ols.06[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[2],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.ols.07[,1],col=ifelse(round(t(eff.ols.07[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[3],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.ols.08[,1],col=ifelse(round(t(eff.ols.08[,1])[1,],2)<1.00,"red","blue"),las=2,xaxt='n')
mtext(side=4,Years[4],cex=0.7)
barplot(cex.names=0.9,horiz=F,cex.axis=0.9,beside=F,eff.ols.09[,1],col=ifelse(round(t(eff.ols.09[,1])[1,],2)<1.00,"red","blue"),las=2)
mtext(side=4,Years[5],cex=0.7)
plot.new()
legend("center",title="Data Envelopement Analysis",fill=c("blue","red"),legend=c("Efficient","Inefficient"),ncol=2)
c
The collection of bar-plots above summarises the efficiency scores for each asset in each of the 5 years of data. In this case we are using OLS derived Fama and French coefficients as inputs to the DEA model for each stock. While the blue bars correspond to efficient stocks, the red bars represent inefficient DMUs.
o
f
The second collection of bar-plots above summarises the efficiency scores for each asset in each of the 5 years of data. In this case we are using QRS derived Fama and French coefficients as inputs to the DEA model for each stock. While the blue bars correspond to efficient stocks, the red bars represent inefficient DMUs. Now that we have determined the subset of the 30 index components that can be deemed efficient in each year using different inputs, let’s construct equally weighted portfolios of these efficient stocks for each year and input set and compare performance. Based on QRS inputs and DEA results, the portfolio constructed in 2009 for example is equally weighted across AXP,IBM,INTL,JNJ, KFT,MSFT,PFE,PG,UTX.
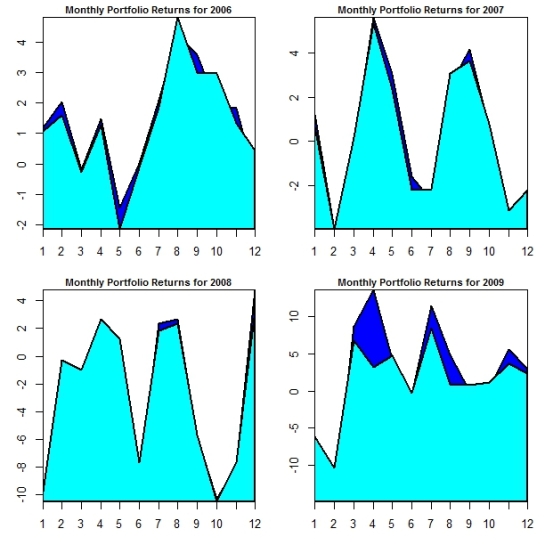
Above is a collection of stacked polygon plots that compares the monthly returns for OLS derived (darkblue) vs QRS derived(cyan) portfolios for 4 years (2006-2009). With the exception of a handful of months in each year, the OLS derived coefficients appear to create superior portfolio returns that the QRS derived counterparts. Only in 2008 , does the QRS portfolio appear to provide some consistency in the benefits of applying a more robust method to the data. As the table below shows,annualising portfolio returns does not seem to help much either. Contrary to expectations the OLS derived portfolio actually is better than the QRS counterpart. The only exception is in 2007-2008 where the QRS portfolio generates less negative returns than the OLS counterpart.
Quantile OLS
2006 15.770552 16.315416
2007 2.443413 3.332335
2008 -31.224554 -35.138542
2009 15.439622 27.783856
f
While the number range is somewhat comparable to those found in the study (link in previous post), we don’t replicate the superiority of QRS portfolios here. The discrepancy is probably due to my mistakes somewhere in the convoluted code. Non the less, it should be noted that the study used the 2005 DJIA components while I used the current index composition. Instead of CISCO and Traveller’s companies, the study had GM and CITI.