Asset Pricing [8f : Replicating Cochrane’s Dog 2]

The previous post outlined the dataset,custom functions used throughout the code as well as some of the intuition behind Cochrane’s(2008) paper. Now we shall continue with the actual implementation of the simulation procedures and steps previously listed.

[1] Obtain original sample estimates (1927-2004) and the error covariance matrix by running the three VAR regressions. This step provides the inputs needed for the subsequent simulation.

After subsetting our original dataset to contain only data for the 1927-2004 date range across transformed variables, I ran the following single period forecasting regressions :

Lowercase variables denote log-transformed variables as usual.The last three equations are the familiar VAR regressions mentioned in previous posts and provide the inputs necessary for the simulation. The first three regressions are just there for completeness sake (they are run by Cochrane as well).These set of equations basically replicate some of the information contained in Tables 1&2 of the paper albeit without inflation adjustments. In the following code, I :

• stored each of the above regressions as an element of a list object.
• The custom RegExtractor)() function is then called to extract regression summaries from this list object using the sapply() function.
• The output is then tabulated using the TableMaker() function.

 

######################################################################################
# Initial single period regression
######################################################################################

#Single Period regressions
initial.reg <- list(
	ret_divyield=dyn$lm(Idx.ret~lag(Div.yield,-1),data=orig.extract),
	exret_divyield=dyn$lm(Exc.ret~lag(Div.yield,-1),data=orig.extract),
	dgrowth_divyield=dyn$lm(Div.growth~lag(Div.yield,-1),data=orig.extract),
	log_ret_divyield=dyn$lm(log.ret~lag(log.div.yield,-1),data=orig.extract),
	log_divgrowth_divyield=dyn$lm(log.div.growth~lag(log.div.yield,-1),data=orig.extract),
	log_divyield_divyield=dyn$lm(log.div.yield~lag(log.div.yield,-1),data=orig.extract)
)
reg.names <- names(initial.reg)

#Extract regression values
betas <- matrix(RegExtractor(initial.reg,'est')[,2],ncol=1)
tvals <- matrix(RegExtractor(initial.reg,'tval')[,2],ncol=1)
pvals <- matrix(RegExtractor(initial.reg,'pval')[,2],ncol=1)
rsq <- matrix(RegExtractor(initial.reg,'rsq'),ncol=1)*100
res <- matrix(RegExtractor(initial.reg,'res'),ncol=6,dimnames=list(NULL,reg.names))
res.cov <- cbind(res[,'log_divgrowth_divyield'],res[,'log_divyield_divyield'])
std.vals <- sapply(initial.reg,function(v) sd(fitted(v)))*100

#Table
col.names <- c('Beta','t-stats','p-vals','R2','Std(Fitted)')
reg.table = cbind(betas,tvals,pvals,rsq,std.vals)

est.tab <- round(reg.table,5)
est.tab <- apply(est.tab, 2, rev)
est.tab <- cbind(rev(reg.names),est.tab)
TableMaker(row.h=1,est.tab,c('Single Period',col.names),strip=F,strip.col=c('green','blue'),col.cut=0.05,alpha=0.7,border.col='lightgrey',text.col='black',header.bcol='gold',header.tcol='black',title=c('Regression on lagged variables\nAnnual data for 1926-2004'))

gg

This results in the following :

The inputs used in the Null hypothesis are

• b(r)=0 and phi=0.94125.The value for phi is simply the coefficient estimate of the log_divyield_divyield regression (last row of table).
• ρ=0.9638 (from the Cochrane paper)
• the dividend forecast coefficient follows from the identity as b(d) = ρφ − 1 + b(r)≈ −0.1
• sample estimates of the covariance matrix from div_growth and div_yield regression.

Such that the Null takes the form of :

 

---

[2 & 3] Each of the 20000 monte carlo trials (50000 in the paper) generates a dataset.Once we have 20000 simulated datasets,we run each of the VAR regressions for each simulated dataset and collect regression estimates.

From the paper : I simulate 20,000 artificial data sets from each null. For φ < 1, I draw the first observation d0 − p0 from the unconditional density d0 − p0 ∼ N(0, σ2(εdp)/(1 − φ^2).For φ ≥ 1, I start at d0 − p0 = 0. I,then draw εdt
and εdpt as random normals and simulate the system forward.

• inputs from the previous step are fed into the MonteCarloSimulation() function which calls the SimulateVAR function() to generate and return the simulated data.
• with each simulated dataset,the MonteCarloSimulation() function continues with our conventional VAR regressions.
• such that for each trial of the simulation we calculate and store the following : b(r),b(d),phi,t-stats for each variable,b(long.r),b(long.d)
• ultimately,the MonteCarloSimulation() function returns a list object with 2 elements.
• the first element is a summary of the inputs used/provided by the user
• the second element of that list contains the simulated results with rows representing trials, and columns representing different stats (e.g. coefficients,tstats)

 

In terms of the code, I have made it such that I only run the simulation once for the sample and once for the fixed case of phi=0.99 (as Cochrane does this too) and save those results, along with the sample regressions and their stats (from step 1), in an RData file.

 

# Run Montecarlo simulation
mcs.sample <- MonteCarloSimulation(num.trials=20000,num.obs=100,phi=betas[6],rho=0.9638,error.cov=res.cov)
mcs.fixed <- MonteCarloSimulation(num.trials=20000,num.obs=100,phi=0.99,rho=0.9638,error.cov=res.cov)

#Save all the sample estimates,and simulation results in a .Rdata file
save(initial.reg,betas,tvals,pvals,rsq,res.cov,mcs.sample,mcs.fixed,file='DogBark.Rdata')

ll

By saving the simulation results we are also saving time.Loading the data back into R is as simple as :

 

#Load data
load('DogBark.Rdata')

lll

So far we have run all the regressions and simulations intended and saved the resulting sample and simulation data in a convenient .RData file for simple access. The next post will examine the marginal and joint distributions of simulated parameter estimates,their respective test statistics as well as long horizon issues and the effects of varying phi on estimates.

Asset Pricing [8e : Replicating Cochrane’s Dog 1]

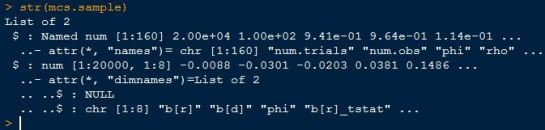
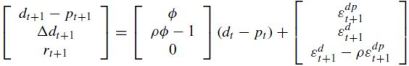In this post I will attempt to replicate some basic results from Cochrane’s(2008) paper ,-‘The Dog that did not bark : a defense of return predictability’ – ; as usual with the posts found on this blog,I do not claim to understand many of the nuances of the paper or the mathematics/statistical procedures behind it (in fact most of it is completely beyond me), it is nevertheless interesting to see how much one can tinker with and replicate using online resources for free.

The present value identity sketched in previous posts establishes the following relationship between [1] dividend yield ,[2] dividend growth and [3] return variables. If the state of the world were such that observed dividend yields are constant over time,then neither return nor dividend growth variables are predictable. Since the state of the world is such that observed dividend yields vary over time,it must be the case that at least one of dividend growth or return is/are predictable. Simple regressions that were run in previous posts establish several main findings (which i shall repeat lest i forget them again) :

1. The dividend price ratio predicts returns but NOT dividend growth.
2. Long-horizon return regressions provide stronger evidence of return predictability than single period counterparts.
3. Returns which should not be forecastable are and dividend growth which should be forecastable isn’t.
4. On average,price dividend ratios are moving in response to expected return news rather than cash flow news.
5. Time varying discount rates explain virtually all the variance of dividend yield while dividend growth forecasts explain essentially none of it.

As has been repeated quite often in these posts on time series predictability: If returns are not predictable, dividend growth must be predictable, to generate the observed variation in dividend yields.The most basic (but nonetheless important) result of Cochrane’s paper that we are going to replicate is the finding that [1] the absence of dividend growth predictability gives stronger evidence than does the presence of return predictability and that [2] long-horizon return forecasts complement single period results. There will be some discrepancies between Cochrane and our results which are probably due to [1] coding errors on my part, [2] not using real (inflation adjusted) variables since they are a hassle to find online (…at least to me), and [3] the use of 20000 monte carlo trials instead of the 50000 used in the paper. Also,I wrote the code almost a year ago and have only come around to blogging about it now,hence many of the issues that may have cropped up at that time are oblivious to me at the moment. This part of the post simply outlines some of the intuitions and procedures behind Cochrane’s paper, as well as the dataset and custom functions used in the code. The subsequent post shall deal with the results obtained and perhaps compare them somewhat to those of the paper.

[Data]

The data used in the code comes from the Chicago Booth advanced investments seminar, which contains [1]Return, [2]Dividend-yield,[3] Dividend-growth and [4] T-bill rate variables. The data file I have goes from 1926 to 2011,the one from the linked site goes to 2012. We only need data from 1927 to 2004, so it doesn’t really matter.After converting the txt file to a csv file in Excel,let’s load it into R,transform some of the variables to the ones we need and subset the data to the date range used in the paper.
ll

#####################################################################################
# Load and extract annual data
#####################################################################################

#Import csv file
orig.csv  <- read.csv('ps1_data.csv',header=T)
orig.ts <- ts(data=orig.csv,start=c(1926),end=c(2011),frequency=1)
orig.extract <- window(orig.ts,start=c(1926),end=c(2004),frequency=1)
orig.extract <- cbind(orig.extract,orig.extract[,1]-orig.extract[,4],log(1+orig.extract[,1]),log(orig.extract[,2]),log(1+orig.extract[,3]))
colnames(orig.extract) <- c('Idx.ret','Div.yield','Div.growth','Tbill.ret','Exc.ret','log.ret','log.div.yield','log.div.growth')

kkk

[Functions]

Functions include: SimulateVAR(),MonteCarloSimulation(),JointPlot(),RegExtractor(),TableMaker(),of which the last two are general helper functions to extract results from regression objects and display tabular information from matrices and such respectively. I don’t know why the code,when copied into wordpress,becomes oddly misaligned at times.
ll

#####################################################################################
#Extract Regression Values
#####################################################################################
RegExtractor <- function(x,type)
{
 if(type=='est'){
  output <- t(sapply(x,function(v)coef(summary(v))[,1]))
 }
 else if (type=='stderr'){
  output <- t(sapply(x,function(v)coef(summary(v))[,2]))
 }
 else if(type=='tval'){
  output <- t(sapply(x,function(v)coef(summary(v))[,3]))
 }
 else if(type=='pval'){
  output <- t(sapply(x,function(v)coef(summary(v))[,4]))
 }
 else if(type=='rsq'){
  output <- t(sapply(x,function(v)(summary(v))$r.squared))
 }
 else if(type=='res'){
  output <- sapply(x,function(v)(resid(v)))
 }
return(output)
}
#####################################################################################


#####################################################################################
# Simulate the VAR
#####################################################################################

SimulateVAR <- function(num.obs,phi,rho,error.cov){
 	dp.sd = round(sqrt(var(error.cov))[2,2],3)
	dg.sd = round(sqrt(var(error.cov))[1,1],2)
	dp.shock = rnorm(num.obs+1,mean=0,sd=dp.sd)
	dg.shock = rnorm(num.obs,mean=0,sd=dg.sd)
	sim.data = matrix(data=0,nrow=num.obs,ncol=3,dimnames=list(NULL,c('sim.divyield','sim.dgrowth','sim.returns')))

	ifelse(phi<1,dp.beg<-rnorm(1,mean=0,sd=dp.sd^2/(1-phi^2)),dp.beg<-0)
  
  sim.data[1,'sim.divyield'] <- phi*dp.beg+dp.shock[2]
  sim.data[1,'sim.dgrowth'] <- ((rho*phi)-1)*dp.beg+dg.shock[1]
	
	for(i in 2:num.obs){
  	sim.data[i,'sim.divyield']<- phi*sim.data[(i-1),'sim.divyield']+dp.shock[i+1]
  	sim.data[i,'sim.dgrowth'] <- ((rho*phi)-1)*sim.data[(i-1),'sim.divyield']+dg.shock[i]
  }
 	sim.data[,'sim.returns'] <- dg.shock-(rho*dp.shock[2:(num.obs+1)])
	return(data.frame(sim.data))
}
#####################################################################################


#####################################################################################
# MonteCarlo
#####################################################################################

MonteCarloSimulation <-function(num.trials,num.obs,phi,rho,error.cov){
	coeff.names <- c('b[r]','b[d]','phi')
	montecarlo.results <- matrix(data=0,nrow=num.trials,ncol=8,dimnames=list(NULL,c(coeff.names,paste(coeff.names,'_tstat',sep=''),c('b[long.r]','b[long.d]'))))
  inputs <- c(num.trials=num.trials,num.obs=num.obs,phi=phi,rho=rho,error.cov=error.cov)

	for(i in 1:num.trials){
		simulated.data <- SimulateVAR(num.obs,phi,rho,error.cov)
		sim.reg <- list(
			dyn$lm(sim.returns~lag(sim.divyield,-1),data=ts(simulated.data)),
			dyn$lm(sim.dgrowth~lag(sim.divyield,-1),data=ts(simulated.data)),
			dyn$lm(sim.divyield~lag(sim.divyield,-1),data=ts(simulated.data))
		)
	  montecarlo.results[i,1:3] <- (RegExtractor(sim.reg,'est')[,2])
		montecarlo.results[i,4:6] <- (RegExtractor(sim.reg,'tval')[,2])
  	montecarlo.results[i,7] <- montecarlo.results[i,1]/(1-rho*montecarlo.results[i,3])
  	montecarlo.results[i,8] <- montecarlo.results[i,7]-1
		
		print(paste('Monte Carlo Simulation :',i))
	}
return(list(inputs,montecarlo.results))
}
#####################################################################################


######################################################################################
# Joint distribution plot
######################################################################################

JointPlot <- function(mc.object,num.points,initial.reg,type){
	
  #Define variables
	betas <- matrix(RegExtractor(initial.reg,'est')[,2],ncol=1)
  tvals <- matrix(RegExtractor(initial.reg,'tval')[,2],ncol=1)
  num.trials <- mc.object[[1]]['num.trials']
	rho <- mc.object[[1]]['rho']
	phi <- betas[6]
  lr.beta <- betas[4]/(1-rho*phi)
	
	if(type=='single period'){
		
		bottom.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']>betas[4] & mc.object[[2]][,'b[d]']<betas[5],)])/num.trials*100
	  top.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']>betas[4] & mc.object[[2]][,'b[d]']>betas[5],)])/num.trials*100
	  bottom.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']<betas[4] & mc.object[[2]][,'b[d]']<betas[5],)])/num.trials*100
	  top.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']<betas[4] & mc.object[[2]][,'b[d]']>betas[5],)])/num.trials*100
	
		plot(ylim=c(min(mc.object[[2]][1:num.points,'b[d]'])-0.15,max(mc.object[[2]][1:num.points,'b[d]'])+0.15),xlim=c(min(mc.object[[2]][1:num.points,'b[r]'])-0.15,max(mc.object[[2]][1:num.points,'b[r]'])+0.15),x=mc.object[[2]][1:num.points,'b[r]'],y=mc.object[[2]][1:num.points,'b[d]'],ylab='b[d]',xlab='b[r]',cex.main=0.85,cex.lab=0.75,cex.axis=0.75,cex=0.65,main=paste('Coefficients\nphi=',mc.object[[1]]['phi']),col='blue',pch=21)
  	abline(h=betas[5])
  	abline(v=betas[4])
		points(x=betas[4],y=betas[5],col='red',cex=1,pch=19)
		points(x=0,y=mc.object[[1]]['rho']*mc.object[[1]]['phi']-1+0,cex=1,pch=17,col='green')
	
		text(x=max(mc.object[[2]][1:num.points,'b[r]']),y=min(mc.object[[2]][1:num.points,'b[d]'])-0.1,paste(bottom.right,'%'),cex=0.75)
		text(x=max(mc.object[[2]][1:num.points,'b[r]']),y=max(mc.object[[2]][1:num.points,'b[d]'])+0.1,paste(top.right,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]']),y=min(mc.object[[2]][1:num.points,'b[d]'])-0.1,paste(bottom.left,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]']),y=max(mc.object[[2]][1:num.points,'b[d]'])+0.1,paste(top.left,'%'),cex=0.75)

		bottom.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]_tstat']>tvals[4] & mc.object[[2]][,'b[d]_tstat']<tvals[5],)])/num.trials*100
		top.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]_tstat']>tvals[4] & mc.object[[2]][,'b[d]_tstat']>tvals[5],)])/num.trials*100
		bottom.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]_tstat']<tvals[4] & mc.object[[2]][,'b[d]_tstat']<tvals[5],)])/num.trials*100
		top.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]_tstat']<tvals[4] & mc.object[[2]][,'b[d]_tstat']>tvals[5],)])/num.trials*100
	
		plot(ylim=c(min(mc.object[[2]][1:num.points,'b[d]_tstat'])-1,max(mc.object[[2]][1:num.points,'b[d]_tstat'])+1),xlim=c(min(mc.object[[2]][1:num.points,'b[r]_tstat'])-1,max(mc.object[[2]][1:num.points,'b[r]_tstat'])+1),x=mc.object[[2]][1:num.points,'b[r]_tstat'],y=mc.object[[2]][1:num.points,'b[d]_tstat'],ylab='tstat,b[d]',xlab='tstat,b[r]',cex.main=0.85,cex.lab=0.75,cex.axis=0.75,cex=0.65,main=paste('T-statistics\nphi=',mc.object[[1]]['phi']),col='blue',pch=21)
  	abline(h=tvals[5])
  	abline(v=tvals[4])
		points(x=tvals[4],y=tvals[5],col='red',cex=1,pch=19)

		text(x=max(mc.object[[2]][1:num.points,'b[r]_tstat']),y=min(mc.object[[2]][1:num.points,'b[d]_tstat'])-0.1,paste(bottom.right,'%'),cex=0.75)
		text(x=max(mc.object[[2]][1:num.points,'b[r]_tstat']),y=max(mc.object[[2]][1:num.points,'b[d]_tstat'])+0.1,paste(top.right,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]_tstat']),y=min(mc.object[[2]][1:num.points,'b[d]_tstat'])-0.1,paste(bottom.left,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]_tstat']),y=max(mc.object[[2]][1:num.points,'b[d]_tstat'])+0.1,paste(top.left,'%'),cex=0.75)

} else if(type=='long horizon'){
     
	  h<-hist(plot=FALSE,mc.object[[2]][,'b[long.r]'],breaks=100)
	  plot(xlim=c(-3,3),h,freq=FALSE,col=ifelse(h$breaks<=lr.beta,'lightgrey','red'),ylab='',xlab='b(r)/(1-rho*phi)',cex.main=0.85,cex.lab=0.75,cex.axis=0.75,cex=0.65,main=paste('phi=',mc.object[[1]]['phi']))
	  abline(v=lr.beta,col='red')
	  text(x=lr.beta+0.3,y=0.45,'Data',col='black',cex=0.75)

		bottom.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']>betas[4] & mc.object[[2]][,'phi']<phi,)])/num.trials*100
	  top.right <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']>betas[4] & mc.object[[2]][,'phi']>phi,)])/num.trials*100
	  bottom.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']<betas[4] & mc.object[[2]][,'phi']<phi,)])/num.trials*100
	  top.left <- length(mc.object[[2]][which(mc.object[[2]][,'b[r]']<betas[4] & mc.object[[2]][,'phi']>phi,)])/num.trials*100
	
    plot(ylim=c(min(mc.object[[2]][1:num.points,'phi'])-0.1,max(mc.object[[2]][1:num.points,'phi'])+0.1),xlim=c(min(mc.object[[2]][1:num.points,'b[r]'])-0.1,max(mc.object[[2]][1:num.points,'b[r]'])+0.1),x=mc.object[[2]][1:num.points,'b[r]'],y=mc.object[[2]][1:num.points,'phi'],ylab='phi',xlab='b[r]',cex.main=0.85,cex.lab=0.75,cex.axis=0.75,cex=0.65,main=paste('phi=',mc.object[[1]]['phi']),col='blue',pch=21)
    abline(h=phi)
  	abline(v=betas[4])
		points(x=betas[4],y=phi,col='red',cex=1,pch=19)
		points(x=0,y=mc.object[[1]]['phi'],cex=1,pch=17,col='green')
	  lines(x=1-rho*mc.object[[2]][,'phi']+betas[5],y=mc.object[[2]][,'phi'],lty='dotted',lwd=0.75,col='gold')
	  lines(x=betas[4]*(1-rho*mc.object[[2]][,'phi'])/(1-phi*rho),col='black',y=mc.object[[2]][,'phi'],lwd=0.75)
  
	  text(x=max(mc.object[[2]][1:num.points,'b[r]']),y=min(mc.object[[2]][1:num.points,'phi'])-0.06,paste(bottom.right,'%'),cex=0.75)
		text(x=max(mc.object[[2]][1:num.points,'b[r]']),y=max(mc.object[[2]][1:num.points,'phi'])+0.06,paste(top.right,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]']),y=min(mc.object[[2]][1:num.points,'phi'])-0.06,paste(bottom.left,'%'),cex=0.75)
		text(x=min(mc.object[[2]][1:num.points,'b[r]']),y=max(mc.object[[2]][1:num.points,'phi'])+0.06,paste(top.left,'%'),cex=0.75)

}
}

################################################################################
#Table Maker
################################################################################

TableMaker <- function(row.h,core,header,strip,strip.col,col.cut,alpha,border.col,text.col,header.bcol,header.tcol,title)
{
	rows <- nrow(core)+1
	cols <- ncol(core)
  colours <- adjustcolor(col=strip.col,alpha.f=alpha)
  idx <- 1
	
	plot.new()
  plot.window(xlim=c(0,cols*11),ylim=c(0,rows*7))
  mtext(title,side=3,cex=0.7)
	
	for(i in 1:cols){
		for(j in 1:rows){
			if(j==1){
       rect((i-1)*11,rows*7-7,11*i,rows*7,density=NA,col=header.bcol,lty=1,border=border.col)
       text(((i-1)*11+11*i)/2,((rows*7-7)+rows*7)/2,header[i],cex=0.8,col=header.tcol,font=1)
			}
			else if((j>1) && (row.h==0))
      {
       rect((i-1)*11,(j-1)*7-7,11*i,(j-1)*7,density=NA,col=ifelse(strip,ifelse(core[j-1,i]<col.cut,colours[1],colours[2]),'white'),lwd=1.0,border=border.col)
       text(((i-1)*11+11*i)/2,(((j-1)*7-7)+(j-1)*7)/2,core[j-1,i],col='black',cex=0.75,font=1)
      }
			else if((j>1) && (row.h!=0) && (i==row.h[idx]))
      {
       rect((i-1)*11,(j-1)*7-7,11*i,(j-1)*7,density=NA,col=border.col,lwd=1.0,border=border.col)
       text(((i-1)*11+11*i)/2,(((j-1)*7-7)+(j-1)*7)/2,core[j-1,i],col='black',cex=0.75,font=1)
			}
			else if((j>1) && (row.h!=0) && (i!=row.h[idx]))
      {
       rect((i-1)*11,(j-1)*7-7,11*i,(j-1)*7,density=NA,col=ifelse(strip,ifelse(core[j-1,i]<col.cut,colours[1],colours[2]),'white'),lwd=1.0,border=border.col)
       text(((i-1)*11+11*i)/2,(((j-1)*7-7)+(j-1)*7)/2,core[j-1,i],col='black',cex=0.75,font=1)
      }
		}
     ifelse(idx<length(row.h),idx<-idx+1,idx<-length(row.h))

	}
}
#####################################################################################
#####################################################################################
#@@@@@@@@@@@@@@@@@@@@@@@@@@@Function Ends@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@#

ll

[Intuition & Procedure]

Cochrane starts with the conventional VAR representation that links log returns,dividend yield and dividend growth variables as seen before:

The Campbell-Shiller (1988) linearisation of returns is then used to link regression coefficients and errors of the VAR such that one can infer the data,coefficients and errors for any one equation from those of the other two :

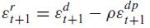
We are interested in learning something about the return predictability coefficient b(r) on the basis of what we can say about phi. In this framework,to generate a coherent null hypothesis with b(r)=0,one must assume a negative b(d) and then address the absence of this coefficient in the data. Essentially this hypothesis will be tested by simulating the VAR under the assumption of no return predictability,b(r)=0 and dividend growth predictability,b(d)=negative. The simulation procedure is as follows (taken from the original paper and other sites such as this presentation) :

[1] Obtain original sample estimates (1927-2004) and the error covariance matrix by running the three VAR regressions. This step provides the inputs needed for the subsequent simulation.

[2] Each of the 20000 monte carlo trials (50000 in the paper) generates a dataset simulated according to the following (shamelessly snipped from the presentation) :

[3] Once we have 20000 simulated datasets,we run each of the VAR regressions for each simulated dataset and collect regression estimates.

[4] Once we have collected regression results across 20000 simulated datasets,we can look at the probability of observing b(r) and b(d) pairs as well as t-statistic pairs that are more extreme than original sample estimates.

[5] Once we have looked at the single period results,we can proceed with the long-horizon regression coefficients ( which are mercifully not new estimates, but rather calculated from the single period estimates of the original sample 1927-2004)

[6] Once we have summarised both single-period and long horizon results ,we can look at the source of power regarding single-period dividend growth coefficients and long horizon tests, as well as examine the effect of varying dividend yield autocorrelation on short- and long run percentage values.