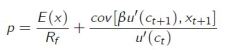The Fama-French 3 factor model is an extension of the market model to the tune of two additional factors to explain security/portfolio returns : the size premium and the book-to-market (value) premium. The model was developed in response to prior research and empirical observations that indicated systematic outperformance of small firm / value stocks versus large firm / growth stocks and the market as a whole. From the previous post it is clear that variation in size produces a variation in average returns that is positively related to variation in market betas, the central risk-return relation posited by the CAPM. By contrast,variation in the book-to-market ratio produces a variation in average returns that is negatively aligned to variation in market betas,violating the central implication of risk-return models.
The Carhart 4 factor model extends the FF3F model with the addition of a momentum factor. The inclusion of this fourth factor is a response to studies that showed how stocks with strong past performance continue to outperform stocks with poor performance in the next period gathering an average excess return of 1% per month (Jegadeesh & Titman,1993)
In some sense, the FF3F model is a synthesis of a string of anomalies that contradict CAPM predictions. The literature surrounding CAPM implications (and more importantly their contradictions) focuses on sorting stocks according to some characteristic (size,value,financial ratios), relating this sorted set of assets with their average returns and econometrically aligning them to market risk. To put the findings in context, the following summarises one of the many literature surveys easily found on the internet.
g
[Survey of contradictions]
:: Earnings/Price Ratio
The earliest blow to the CAPM came from Basu(1977) who showed that stocks with high E/P ratios earned significantly higher returns than assets with low E/P ratios. Since differences in beta could not explain these return differences,the E/P effect is a direct contradiction of the CAPM.
:: Firm Size
The size effect,uncovered by Banz(1981),indicates that stocks of firms with low market capitalisations have higher average returns than large cap stocks. While smaller firms also suffer from greater market risk and hence preserve a positive risk-return relation required by theory, the beta differences are unfortunately not large enough to explain the observed return differences to conform to CAPM predictions.
:: Long-Term Return Reversals
Defining ‘losers’ as stocks that have had poor returns over the past 3-5 years and ‘winners’ as those stocks that had high returns over a similar period,Debondt and Thaler(1985) found that losers tend to have much higher average returns than winners over the next 3 to 5 years. The key question,of whether or not the superior returns associated with looser stocks are aligned with higher systematic risk, had been settled in the early 1990s by Lakonishok and Ritter (1992) who suggested that the variation in beta cannot account for this difference in average returns between losers and winners.
:: Book-to-Market Ratio
Rosenberg,Reid and Lanstein(1985) found that stocks with high book-to-market ratios have significantly higher returns than stocks with lower values for this ratio. This variable still produces significant dispersion in average returns that cannot be explained with the CAPM alone.
:: Leverage
Bhandri(1988) found that firms with high leverage (measured by the debt/equity ratio) have higher average returns than firms with less debt even after controlling for size and market beta. The increased riskiness of a highly leveraged firm’s equity should be reflected in a higher beta coefficient.
:: Momentum
Jegadeesh and Titman (1993) found that stock returns tend to exhibit short-term momentum. Momentum tends to be stronger for firms that have had poor recent performance. This pattern is opposite of that found in the long-term overreaction studies where long-term losers outperform long term winners.
This blog post simply extends the FF3F model examined previously with a momentum factor (that can be downloaded from Kenneth French’s data library for free). A different subset of the 25 size/value sorted portfolios shall be used here : Jan 1932 – Dec 2002. The code is largely the same with small amendments made to include the 4th factor in regressions and additional plots for the Carhart model.
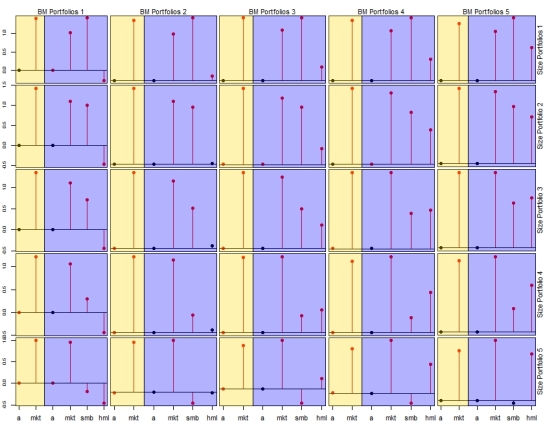
First a collective plot of the excess returns across 25 portfolios as before but using a different subset.
Following a time series regression for the 3 models (CAPM,FF3F,Carhart), let’s summarise the estimated intercepts and goodness of fit statistics for the 25 portfolios and provide a table of R-squared measures for the FF3F and Carhart models to better observe the differences.
#Store Rsq and alpha values in matrix across models
border.names <- list(c(paste('Size',1:5)),c(paste('Value',1:5)))
Rsq.mat.capm <- NULL
Rsq.mat.ff <- NULL
Rsq.mat.car <- NULL
for(i in 1:5){
Rsq.mat.capm <- rbind(Rsq.mat.capm,SZ.BM$size.excess[[i]]$capm.rsq)
Rsq.mat.ff <- rbind(Rsq.mat.ff,SZ.BM$size.excess[[i]]$ff.rsq)
Rsq.mat.car <- rbind(Rsq.mat.car,SZ.BM$size.excess[[i]]$car.rsq)
}
dimnames(Rsq.mat.capm) <- border.names
dimnames(Rsq.mat.ff) <- border.names
dimnames(Rsq.mat.car) <- border.names
alpha.mat.capm <- NULL
alpha.mat.ff <- NULL
alpha.mat.car <- NULL
for(i in 1:5){
alpha.mat.capm <- cbind(alpha.mat.capm,SZ.BM$size.excess[[i]]$ts.alpha)
alpha.mat.ff <- cbind(alpha.mat.ff,SZ.BM$size.excess[[i]]$ff.alpha)
alpha.mat.car <- cbind(alpha.mat.car,SZ.BM$size.excess[[i]]$car.alpha)
}
alpha.mat.capm <- t(alpha.mat.capm)
alpha.mat.ff <- t(alpha.mat.ff)
alpha.mat.car <- t(alpha.mat.car)
dimnames(alpha.mat.capm) <- border.names
dimnames(alpha.mat.ff) <- border.names
dimnames(alpha.mat.car) <- border.names
#Collective plots for alphas and Rsquared
windows()
layout(matrix(c(1,2,3,4,5,6,7,8,9,10,rep(11,5),rep(12,5)),nrow=4,ncol=5,byrow=T))
for(i in 1:5){
par(mai=c(0.05,0.1,0.5,0.1))
plot(cex.main=0.85,cex.lab=0.35,cex.axis=0.65,main=paste('Size Quintile',i),x=1:5,y=alpha.mat.capm[i,],'b',col='darkgreen',lwd=1,xaxt='n',yaxt='n',ylab='',xlab='')
abline(h=0,col='darkgrey',lwd=2)
lines(x=1:5,y=alpha.mat.ff[i,],'o',col='red',lwd=1)
lines(x=1:5,y=alpha.mat.car[i,],'o',col='blue',lwd=1)
legend(title='TS-Alphas','topleft',fill=c('darkgreen','blue','red','darkgrey'),legend=c('CAPM','FF3F','CARHART','Zero value'),ncol=1,bg='white',bty='n',cex=0.6)
}
for(i in 1:5){
par(mai=c(0.5,0.1,0.1,0.05))
plot(cex.main=0.85,cex.lab=0.35,cex.axis=0.65,x=1:5,y=Rsq.mat.capm[i,],'b',col='darkgreen',lwd=1,xaxt='n',yaxt='n',ylab='',xlab='',ylim=c(0.3,1))
axis(side=1,labels=paste('V',1:5),at=1:5,cex.axis=0.8)
abline(h=0,col='darkgrey',lwd=2)
lines(x=1:5,y=Rsq.mat.ff[i,],'o',col='red',lwd=1,lty=4)
lines(x=1:5,y=Rsq.mat.car[i,],'o',col='blue',lwd=1,lty=2)
legend(title='Rsquared','bottomleft',fill=c('darkgreen','blue','red'),legend=c('CAPM','FF3F','CARHART'),ncol=1,bg='white',bty='n',cex=0.6)
}
#Tablemaker for Rsquared
ff.tab <- matrix(round(Rsq.mat.ff,5),ncol=5)
ff.tab <- apply(ff.tab, 2, rev)
ff.tab <- cbind(rev(rownames(Rsq.mat.ff)),ff.tab)
par(mai=c(0.25,0.1,0.15,0.1))
TableMaker(row.h=1,ff.tab,c('Portfolios',border.names[[2]]),strip=F,strip.col=c('red','green'),col.cut=0,alpha=0.7,border.col='lightgrey',text.col='black',header.bcol='red',header.tcol='white',title='Goodness of Fit for FF3F')
car.tab <- matrix(round(Rsq.mat.car,5),ncol=5)
car.tab <- apply(car.tab, 2, rev)
car.tab <- cbind(rev(rownames(Rsq.mat.car)),car.tab)
par(mai=c(0.25,0.1,0.15,0.1))
TableMaker(row.h=1,car.tab,c('Portfolios',border.names[[2]]),strip=F,strip.col=c('red','green'),col.cut=0,alpha=0.7,border.col='lightgrey',text.col='black',header.bcol='red',header.tcol='white',title='Goodness of Fit for Carhart')
jik
The first row of line plots show estimated time series intercepts for all 3 models across size quintiles. Visual inspection suggests the multifactor models to provide lower values for the alpha term than the CAPM. Ofcourse p-values have been computed too,but I have not plotted them here. The second row of line plots shows how the goodness of fit measure (R-squared) varies according to the fitted models across the 25 double sorted portfolios. While the multifactor models tend to outperform the single factor model,especially in relation to small sized portfolios (size quintile 1 for instance),the distinction between the FF3F and Carhart models is less apparent from visual inspection,motivating a tabular representation of the same below the set of described plots. The Carhart model tends to do a bit better when it comes to smaller size and lower value portfolios.
For a high quality pdf file click here.
As before,to illustrate the failure of the CAPM in explaining double sorted portfolios (but applied to a different subset of the original data), I plot the average excess returns against CAPM beta. Interpretation is as before with a negative relation between risk and return within a size quintile and across growth/value portfolios signifying the failure of the single index model.
Finally,a set of plots charting average excess returns against model predictions are made to visualise the cross sectional fits.
####################################################################################
#Fitted vs Actual
####################################################################################
windows()
layout(matrix(c(1,2,3,4,5,6),ncol=2,byrow=F))
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[Size Focus]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
#CAPM
par(mai=c(0.1,0.325,0.3,0.1))
plot(x=SZ.capm.fitted*100,y=SZ.focus*100,xlab='',xaxt='n',ylab='',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=SZ.capm.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=SZ.capm.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('CAPM\n',paste('[Rsq',round(SZ.capm.rsq,4)*100,'%]'),'\n\nLines connect same\n Size Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Smallest Size Portfolio',paste('Size Portfolio',2:4),'Largest Size Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
mtext(cex=0.85,adj=-0.7,side=3,paste('Actual versus Predicted Excess Returns for the period',sub.c.1[1],'-',sub.c.2[1]))
#Fitted 3 factor models
par(mai=c(0.1,0.325,0.1,0.1))
plot(x=SZ.ff.fitted*100,y=SZ.focus*100,xlab='',xaxt='n',ylab='',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=SZ.ff.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=SZ.ff.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('Fama & French Model\n',paste('[Rsq',round(SZ.ff.rsq,4)*100,'%]'),'\n\nLines connect same\n Size Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Smallest Size Portfolio',paste('Size Portfolio',2:4),'Largest Size Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
#mtext(font=2,line=2,cex=0.75,text='25 Size/BM sorted Portfolios : Actual average excess returns against model predictions',side=2)
#Fitted 4 factor models
par(mai=c(0.3,0.325,0.1,0.1))
plot(x=SZ.car.fitted*100,y=SZ.focus*100,xlab='',ylab='',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=SZ.car.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=SZ.car.fitted[beg[i]:end[i]]*100,y=SZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('Carhart Model\n',paste('[Rsq',round(SZ.car.rsq,4)*100,'%]'),'\n\nLines connect same\n Size Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Smallest Size Portfolio',paste('Size Portfolio',2:4),'Largest Size Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
#**************************************************************************************************#
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[Value Focus]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
#CAPM
par(mai=c(0.1,0.1,0.3,0.325))
plot(x=BZ.capm.fitted*100,y=BZ.focus*100,xlab='',ylab='',xaxt='n',yaxt='n',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=BZ.capm.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=BZ.capm.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('CAPM\n',paste('[Rsq',round(SZ.capm.rsq,4)*100,'%]'),'\n\nLines connect same\n Book Market Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Lowest Value Portfolio',paste('Value Portfolio',2:4),'Highest Value Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
#Fitted 3 factor models
par(mai=c(0.1,0.1,0.1,0.325))
plot(x=BZ.ff.fitted*100,y=BZ.focus*100,xlab='',ylab='',yaxt='n',xaxt='n',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=BZ.ff.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=BZ.ff.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('Fama & French Model\n',paste('[Rsq',round(SZ.ff.rsq,4)*100,'%]'),'\n\nLines connect same\n Book Market Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Lowest Value Portfolio',paste('Value Portfolio',2:4),'Highest Value Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
#Fitted 4 factor models
par(mai=c(0.3,0.1,0.1,0.325))
plot(x=BZ.car.fitted*100,y=BZ.focus*100,xlab='',ylab='',yaxt='n',cex.main=0.85,cex.lab=0.7,cex.axis=0.65,xlim=c(0.5,1.7),ylim=c(0.2,1.7),col='white')
for(i in 1:5){
lines(x=BZ.car.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i])
points(x=BZ.car.fitted[beg[i]:end[i]]*100,y=BZ.focus[beg[i]:end[i]]*100,col=cols.m[i],pch=20+i)
}
abline(0,1)
legend(title=paste('Carhart Model\n',paste('[Rsq',round(SZ.car.rsq,4)*100,'%]'),'\n\nLines connect same\n Book Market Quintile'),'bottomright',pch=21:25,col=cols.m,legend=c('Lowest Value Portfolio',paste('Value Portfolio',2:4),'Highest Value Portfolio'),ncol=1,bg='white',bty='n',cex=0.7)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
For a better view click here